[SCOI2005]扫雷

题目描述

相信大家都玩过扫雷的游戏。那是在一个$n\times m$的矩阵里面有一些雷，要你根据一些信息找出雷来。万圣节到了，“余”人国流行起了一种简单的扫雷游戏，这个游戏规则和扫雷一样，如果某个格子没有雷，那么它里面的数字表示和它8连通的格子里面雷的数目。现在棋盘是$n\times 2$的，第一列里面某些格子是雷，而第二列没有雷，如下图：

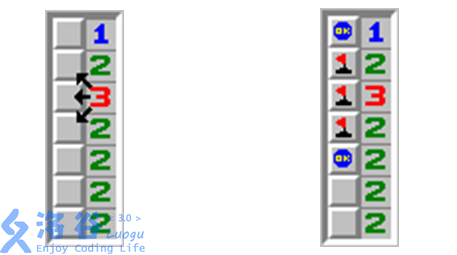
由于第一列的雷可能有多种方案满足第二列的数的限制，你的任务即根据第二列的信息确定第一列雷有多少种摆放方案。

输入格式

第一行为N，第二行有N个数，依次为第二列的格子中的数。（1<= N <= 10000）

输出格式

一个数，即第一列中雷的摆放方案数。

样例 #1

样例输入 #1

1
2
2
1  1

样例输出 #1

1
2

题解

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <iostream>

using namespace std;

int p[10010],a[10010],N,ans=2;

void solve(){
    for(int i=2;i<=N+1;i++){
        p[i] = a[i-1]-p[i-1]-p[i-2];
        if(!(p[i] == 1 || p[i] == 0)){
            --ans;
            break;
        }
        if(i == N+1 && p[i] != 0){
            --ans;
            break;
        }
    }
}

int main(){
    cin >> N;
    for(int i=1;i<=N;i++) cin >> a[i];
    p[1] = 1;
    solve();
    p[1] = 0;
    solve();
    cout << ans << endl;
    return 0;
}

思路

关键在于：

1
p[i] = a[i-1]-p[i-1]-p[i-2];

如果这个递推式子想到了的话就成了，注意最后一行只会出现 $1，2$ 两个情况，所以说再往下的 $N+1$ 行的 $p$ 数组必定是 $0$ .

一开始没想出来，又双叒叕是看的别人的题解.