补题 Codeforces Round 881 (Div. 3)

D. Apple Tree

Timofey has an apple tree growing in his garden; it is a rooted tree of $n$ vertices with the root in vertex $1$ (the vertices are numbered from $1$ to $n$). A tree is a connected graph without loops and multiple edges.

This tree is very unusual — it grows with its root upwards. However, it’s quite normal for programmer’s trees.

The apple tree is quite young, so only two apples will grow on it. Apples will grow in certain vertices (these vertices may be the same). After the apples grow, Timofey starts shaking the apple tree until the apples fall. Each time Timofey shakes the apple tree, the following happens to each of the apples:

Let the apple now be at vertex $u$.

  • If a vertex $u$ has a child, the apple moves to it (if there are several such vertices, the apple can move to any of them).
  • Otherwise, the apple falls from the tree.

It can be shown that after a finite time, both apples will fall from the tree.

Timofey has $q$ assumptions in which vertices apples can grow. He assumes that apples can grow in vertices $x$ and $y$, and wants to know the number of pairs of vertices ($a$, $b$) from which apples can fall from the tree, where $a$ — the vertex from which an apple from vertex $x$ will fall, $b$ — the vertex from which an apple from vertex $y$ will fall. Help him do this.

Input

The first line contains integer $t$ ($1 \leq t \leq 10^4$) — the number of test cases.

The first line of each test case contains integer $n$ ($2 \leq n \leq 2 \cdot 10^5$) — the number of vertices in the tree.

Then there are $n - 1$ lines describing the tree. In line $i$ there are two integers $u_i$ and $v_i$ ($1 \leq u_i, v_i \leq n$, $u_i \ne v_i$) — edge in tree.

The next line contains a single integer $q$ ($1 \leq q \leq 2 \cdot 10^5$) — the number of Timofey’s assumptions.

Each of the next $q$ lines contains two integers $x_i$ and $y_i$ ($1 \leq x_i, y_i \leq n$) — the supposed vertices on which the apples will grow for the assumption $i$.

It is guaranteed that the sum of $n$ does not exceed $2 \cdot 10^5$. Similarly, It is guaranteed that the sum of $q$ does not exceed $2 \cdot 10^5$.

Output

For each Timofey’s assumption output the number of ordered pairs of vertices from which apples can fall from the tree if the assumption is true on a separate line.

Examples

input

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
2
5
1 2
3 4
5 3
3 2
4
3 4
5 1
4 4
1 3
3
1 2
1 3
3
1 1
2 3
3 1

output

1
2
3
4
5
6
7
2
2
1
4
4
1
2

input

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
2
5
5 1
1 2
2 3
4 3
2
5 5
5 1
5
3 2
5 3
2 1
4 2
3
4 3
2 1
4 2

output

1
2
3
4
5
1
2
1
4
2

Note

In the first example:

  • For the first assumption, there are two possible pairs of vertices from which apples can fall from the tree: $(4, 4), (5, 4)$.
  • For the second assumption there are also two pairs: $(5, 4), (5, 5)$.
  • For the third assumption there is only one pair: $(4, 4)$.
  • For the fourth assumption, there are $4$ pairs: $(4, 4), (4, 5), (5, 4), (5, 5)$.

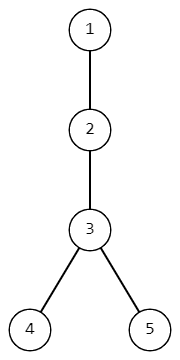
Tree from the first example.

For the second example, there are $4$ of possible pairs of vertices from which apples can fall: $(2, 3), (2, 2), (3, 2), (3, 3)$. For the second assumption, there is only one possible pair: $(2, 3)$. For the third assumption, there are two pairs: $(3, 2), (3, 3)$.

题解

题目解析

上面说了许多，其实说实话就是给你一个二叉树型图，你需要去找到苹果所在的节点和他的子树一共有多少个叶子节点.其中一个坑点我也踩了:就是除了根节点是1之外,其他的节点都是随机连接的,也就是说我们需要用无向图存.我一开始用的有向图存结果有个测试点整个WA了.

再一个就是我从这道题学到了有向图和无向图的DFS和它们的差别,图论学习任重而道远.

把每个节点所在子树的所有叶子节点个数存下来,题目给了两个苹果.我们只需要利用乘法原理就可以得到总的方案数是两个子树叶子节点个数相乘.

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include <iostream>
#include <cstring>
#include <cmath>
#include <string>
#include <queue>
#include <vector>
#include <algorithm>
using namespace std;

#define endl "\n"
#define CIN_ ios::sync_with_stdio(0)
#define CIN cin.tie(0)
#define MAXN(size) const long long MAXN = size + 100
#define mem(name,value) memset(name,value,sizeof(name))
#define fa(a,n,p) for(int i=a;i<=n;i+=p)
#define fb(a,n,p) for(int i=a;i>=n;i-=p)
#define cin(length,var) for(int i=1;i<=length;i++) cin >> var[i]
#define T_ int T;cin >> T;while(T--)
typedef long long ll;
typedef unsigned long long ull;

MAXN(4e5);//本来是开2e5,由于无向图就需要两倍了.

struct ty{//链式前向星
	int t,next;
}edge[MAXN];

int head[MAXN],head_cunt[MAXN],cunt=0;

void addedge(int heads,int child){
	edge[++cunt].t = child;
	edge[cunt].next = head[heads];
	head[heads] = cunt;
}

void dfs(int node,int parent){
	head_cunt[node] = 0;

	for(int i=head[node];i;i=edge[i].next){
		int child = edge[i].t;
		if(child != parent){
			dfs(child,node);
			head_cunt[node] += head_cunt[child];
		}
	}

	if(head_cunt[node] == 0) head_cunt[node] = 1;
}

signed main(){
    CIN;CIN_;
    T_{
    	int n;
    	cin >> n;
    	fa(1,n-1,1){
    		int x,y;
    		cin >> x >> y;
    		addedge(x,y);
    		addedge(y,x);
    	}
    	dfs(1,-1);//遍历的时候把父节点设置为-1的话就不会发生把根节点当成叶子节点的情况了
    	cin >> n;
    	fa(1,n,1){
    		int x,y;
    		cin >> x >> y;
    		cout << (ll)head_cunt[x]*head_cunt[y] << endl;
    	}
    	mem(head,0);
    	cunt = 0;
    }
    return 0;
}